JEE 2016 :: Advanced 2016 :: Mathematics 2016

• Advanced 2016 - Physics 2016
• Advanced 2016 - Chemistry 2016
• Advanced 2016 - Mathematics 2016

Let   $P=\begin{bmatrix}3 & -1 &-2\\2 & 0 &\alpha\\3&-5&0\end{bmatrix}$  , where  $\alpha \epsilon R$ .Suppose Q= [$q_{ij}$] is a matrix such that  PQ=kl, where  $k\epsilon R, k\neq 0$ and l is the identity matrix of order 3. If  $q_{23}=-\frac{k}{8}$  and $det(Q)=\frac{k^{2}}{2}$  then

Answer:

Explanation:

Here,  $P=\begin{bmatrix}3 & -1 &-2\\2 & 0 &\alpha\\3&-5&0\end{bmatrix} $

 Now,   $|P|=3(5\alpha)+1(-3\alpha)-2(-10)=12\alpha+20$         ...........(i)

$\therefore$    adj(P)=   $\begin{bmatrix}5\alpha & 2\alpha &-10\\-10 & 6 &12\\\alpha&-(3\alpha+4)&2\end{bmatrix} ^{T}$

 =  $\begin{bmatrix}5\alpha & -10 &-\alpha\\2\alpha & 6 &-3\alpha-4\\-10&12&2\end{bmatrix}$   .....(ii)

 As,  PQ=kI

 $\Rightarrow$    $|P||Q|=|kI|$

 $\Rightarrow$    $|P||Q|=k^{3}$

 $\Rightarrow$    $|P|\left(\frac{k^{2}}{2}\right)=k^{3}$     $\left[ given, |Q|=\frac{k^{2}}{2}\right]$

 $\Rightarrow$  |P|=2k    ..............(iii)

$\because$             PQ=ki

$\because$           $Q= kp^{-1}I$

$=k.\frac{adjP}{|P|}=\frac{k(adjP)}{2k}$   [ from Eq. (iii)]

 $=\frac{adjP}{2}$

 $=\frac{1}{2}\begin{bmatrix}5\alpha & -10 &-\alpha\\2\alpha & 6 &-3\alpha-4\\-10&12&2\end{bmatrix}$

 $\therefore$    $q_{23}=\frac{-3\alpha-4}{2} \left[ given, q_{23}=-\frac{k}{8}\right]$

$\Rightarrow$              $-\frac{(3\alpha+4)}{2}=-\frac{k}{8}$

 $\Rightarrow$    $(3\alpha+4)\times 4=k$

$\Rightarrow$   $12\alpha+16=k$       .......(iv)

From Eq .(iii) . |P|=2k

 $\Rightarrow$   $12\alpha +20=2k$

Let  $f:(0,\infty)\rightarrow R$ be a differentiable function such that   $f'(x)=2-\frac{f(x)}{x}$  for all  $x \epsilon (0,\infty)$  and $f(1)\neq 1$ Then

Answer:

Explanation:

Here,  $f'(x)=2-\frac{f(x)}{x}$ 

   or      $\frac{\text{d}y}{\text{d}x}+\frac{y}{x}=2$

  [i.e , linear  differential  equation in y]

 Integrationg Factor. IF

               $=\int_{e}^{1/x} dx=e^{\log x}=x$

  $\therefore$   Required solution is 

  $y.(IF)=\int_{}^{} Q(IF)dx+C$

$\Rightarrow$    $y(x)=\int_{}^{}2(x)dx+C $

  $\Rightarrow$    $yx= x^{2}+C$

  $\therefore$  $y=x+\frac{C}{x}$    $[\therefore C\neq 0,asf(1)\neq1]$

  (a)   $\lim_{x \rightarrow 0+}f'(\frac{1}{x})=\lim_{x \rightarrow 0+}(1-Cx^{2})=1$  

            $\therefore$  Option (a) is correct.

(b)   $\lim_{x \rightarrow 0+}xf(\frac{1}{x})=\lim_{x \rightarrow 0+}(1+Cx^{2})=1$

                   $\therefore$   Option (b) is incorrect.

(c)    $\lim_{x \rightarrow 0+}x^{2}f'(x)=\lim_{x \rightarrow 0+}(x^{2}-C)=-C\neq 0$

                 $\therefore$  Option (c) is incorrect.

(d)    $f(x)=x+\frac{C}{x},C\neq0$

            For C>0,    $\lim_{x \rightarrow 0+}f(x)=\infty$

    $\therefore$ Function is not bounded in (0,2)

  $\therefore$    Option (d) is incorrect.

Let  $f:R\rightarrow R,g:R\rightarrow R$ and  $h:R\rightarrow R$ be differentiable functions such that  $f(x)=x^{3}+3x+2$, $g(f(x))=x$   and  $h(g(g(x)))=x$ for all  $x \epsilon R$   , Then

Answer:

Explanation:

As  , g(f(x))=x

Thus, g(x) is inverse of f(x)

$\Rightarrow$    g(f(x))=x

$\Rightarrow$     $g'(f(x)).f'(x)=1$

$\therefore$     $g'(f(x))=\frac{1}{f'(x)}$             ............(i)

 [ where, $f'(x)=3x^{2}+3$ ]

when    f(x)=2, then

 $x^{3}+3x+2=2$

$\Rightarrow$    x=0

 i.e, when x=0 , then f(x)=2

$\therefore$    $g'(f(x))=\frac{1}{3x^{2}+3}$  at (0,2)

$\Rightarrow$   $g'(2)=\frac{1}{3}$

$\therefore$   Option  (a) is incorrect.

Now,   $h(g(g(x)))=x$

 $\Rightarrow$    $h(g(g(f(x)))=f(x)$

 $\Rightarrow$   $h(g(x))=f(x)$            ......(ii)

As   $g(f(x))=x$ 

 $\therefore$     $h(g(3))=f(3)=3^{3}+3(3)+2=38$

 $\therefore$   Option (d) is incorrect.

 From Eq.(ii).

h(g(x))=f(x)

 $\Rightarrow$   $ h(g(f(x)))= f(f(x))$

$\Rightarrow$    $h(x)=f(f(x))$    .......(iii)

[using g(f(x))=x]

$\Rightarrow$   $h'(x)=f'(f(x)).f'(x)$         .........(iv)

Putting x=1, we get

$h'(1)=f'(f(1)).f'(1)$

$=(3\times 36+3)\times 6$

=  $111\times 6=666$

  $\therefore$    Option (b) is correct.

  Putting x=0 in E.q. (iii) , we get

   $h(0)=f(f(0))=f(2)$

   =8+6+2=16

 $\therefore$  Option (c) is correct.

The circle $C_{1}:x^{2}+y^{2}=3$   with  centre at O intersects the parabola $x^{2}=2y$ at point P in the first quadrant .Let the tangent to the circle   $C_{1}$ at P touches other two circles  $C_{2}$  and $C_{3}$  at $R_{2}$  and  $R_{3}$  , respectively. Suppose  $C_{2}$  and $C_{3}$  have equal radii  $2\sqrt{3}$ and centres   $Q_{2}$ and  $Q_{3}$ , respectively. If $Q_{2}$  and  $Q_{3}$  lie on the Y-axis , then

Answer:

Explanation:

Given,

   $C_{1}:x^{2}+y^{2}=3$   intersects the parabola $x^{2}=2y$

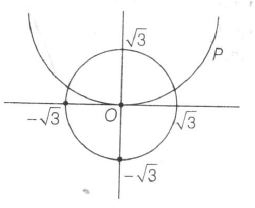
 On solving  $x^{2}+y^{2}=3$  and  $x^{2}=2y$

 get

 $y^{2}+2y=3$

  $\Rightarrow$     $y^{2}+2y-3=0$

$\Rightarrow$    $(y+3)(y-1)=0$

$\therefore$      y=1,-3

[ neglecting y=-3,as   $-\sqrt{3}\leq y\leq\sqrt{3}$  ]

$\therefore$    y=1

$\Rightarrow$           $x=\pm\sqrt{2}$

 $\Rightarrow$    $P(\sqrt{2},1)\epsilon $I  quadrant.

Equation of tangent at  $P(\sqrt{2},1)$   to   $C_{1}:x^{2}+y^{2}=3$ is 

 $\sqrt{2}x+1.y=3$           ............(i)

Now, let the centres of  $C_{2}$ and $C_{3}$ be  $Q_{2}$ and  $Q_{3}$, and tangent P touches  $C_{2}$  and $C_{3}$ , at 

$R_{2}$  and  $R_{3}$  shown in below

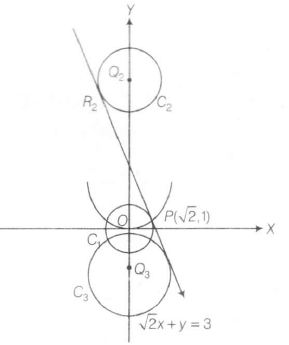
Let  $Q_{2}$ be (o,k) and radius is  $2\sqrt{3}$

$\therefore$    $\frac{|0+k-3|}{\sqrt{2+1}}=2\sqrt{3}$

   $\Rightarrow$     $|k-3|=6\Rightarrow k=9,-3$

 $Q_{2}$ (0,9)  and  $Q_{3}$ (0,-3)

 Hence, $Q_{2}$$Q_{3}$=12

 $\therefore$   Option (a) is correct.

Also,   $R_{2}$  $R_{3}$    is common internal tangent to   $C_{2}$  and $C_{3}$

 and   $r_{2}=r_{3}=2\sqrt{3}$

 $R_{2}R_{3}=\sqrt{d^{2}-(r_{1}+r_{2})^{2}}$

=  $R_{2}R_{3}=\sqrt{12^{2}-({4\sqrt{3}})^{2}}$

 $=\sqrt{144-48}=\sqrt{96}=4\sqrt{6}$

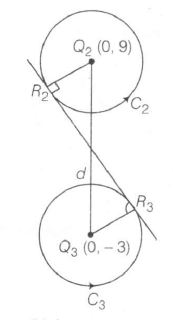
  $\therefore$    Option (b) is correct

 $\therefore$      Length of perpendicular from O(0,0) to  $R_{2}$  $R_{3}$  is equal to radius   $C_{1}=\sqrt{3}$

   $\therefore$     area of $\triangle OR_{2}R_{3}$ =   $\frac{1}{2}\times R_{2}R_{3}\times\sqrt{3}$

  =   $\frac{1}{2}\times 4\sqrt{6}\times\sqrt{3}$

  =  $6\sqrt{2}$

$\therefore$  Option (c) is correct

    Also  , area of  $\triangle PQ_{2}Q_{3}$  =  $\frac{1}{2}Q_{2}.Q_{3}\times\sqrt{2}$

    =  $\frac{1}{2}\times12\times\sqrt{2}=6\sqrt{2}$

  $\therefore$    Option (d) is incorrect.  

Let RS be the diameter of the circle  $x^{2}+y^{2}=1$, where S is the point (1,0). Let P be a variable point (other than R and S) on the circle and tangents to be a circle at S and P meet at the point Q. The normal to the circle at P.intersects  a  line drawn through Q parallel to RS at point  E.  Then, the locus of E passes through the point (s)

Answer:

Explanation:

Given, RS is the diameter of  $x^{2}+y^{2}=1$,

Here , equation of the tangent at   $P(\cos\theta,\sin\theta)$  is   $x\cos\theta+y\sin\theta=1$

Intersecting with x=1

$y=\frac{1-\cos\theta}{\sin \theta}$

 $\therefore$     $Q\left(1.\frac{1-\cos\theta}{\sin\theta}\right)$

$\therefore$  Equation of the line through Q parallel to RS is

 $y=\frac{1-\cos \theta}{\sin\theta}=\frac{2\sin^{2}\frac{\theta}{2}}{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}=\tan\frac{\theta}{2}$                      ............( i)

Normal at   $P:y=\frac{\sin\theta}{\cos\theta}.x$

 $\Rightarrow$   $y=x\tan\theta$                 ...........(ii)

Let their point of intersection be (h,k),

Then,    $k=\tan\frac{\theta}{2}$  and  $k=h\tan\theta$

$\therefore$   $k=h\left(\frac{2\tan\frac{\theta}{2}}{1-\tan^{2}\frac{\theta}{2}}\right)$

$\Rightarrow$    $k=\frac{2h.k}{1-k^{2}}$

$\Rightarrow$   $k(1-k^{2})=2hk$

 $\therefore$ Locus  for point  $E:2x=(1-y^{2})$   .....(iii)

when  $x=\frac{1}{3}$

then    $1-y^{2}=\frac{2}{3}$

$\Rightarrow$             $y^{2}=1-\frac{2}{3}$

$\Rightarrow$       $y=\pm\frac{1}{\sqrt{3}}$

$\therefore \left(\frac{1}{3},\pm\frac{1}{\sqrt{3}}\right)$   satisfy $2x=1-y^{2}$

when  $x=\frac{1}{4},$  then

$1-y^{2}=\frac{2}{4}$

$\Rightarrow$         $y^{2}=1-\frac{1}{2}$

$\Rightarrow$             $y=\pm\frac{1}{\sqrt{2}}$

$\therefore\left(\frac{1}{4},\pm\frac{1}{2}\right)$   does not satisfy  $1-y^{2}=2x$

• Advanced 2016 - Physics 2016
• Advanced 2016 - Chemistry 2016
• Advanced 2016 - Mathematics 2016